Explaining the components of a Neural Network [AI]

Machine Learning

Artificial neural networks are part of the field machine learning.

Connection to Biology

Neural networks in machine learning were inspired and are based on biological neural networks. That's why you will find some shared vocabulary and biological terms that you otherwise might not expect in computer science.

The idea was that human brains were much more adapt at solving certain problems than conventional algorithms and researchers thought they could use the architecture of our brains to make machines more efficient in solving these problems.

Basic Structure

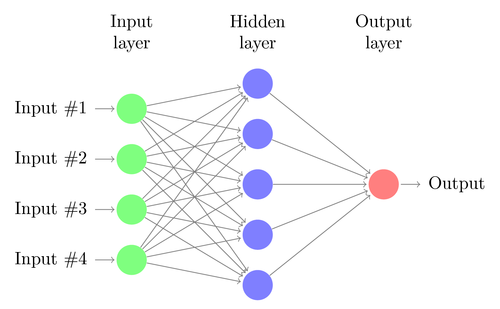
Neurons

The basic building block of a neural network is the neuron - or also called the node. The essentials:

• neurons most often have multiple inputs $x_i$
• they only have one output $y$
• by calculating \(\sum_i w_i * x_i = y\)

If you compare this with the above basic structure of a network, you might notice, that in that image the nodes have multiple outgoing edges. That just means that the single output is sent to multiple nodes in the next layer as input. The node just computes one value, but that value can be used multiple times.

Connections/Weights

The neurons are connected with edges and each edge represents a weight $w$. So for each node every input gets a weight, which is the number with which the input is multiplied before all inputs are added up.

$$\sum_i w_i * x_i = y$$

At the start of training, the weights are unknown and will be adjusted by trial and error (or with more useful methods like gradient descent). A known data point will be inserted into the network and the result will be compared to the true result $y$ and if it is wrong, the weights need to be changed.

Layers

A layer consists of some neurons all at the same depth in the network. A network can have arbitrarily many layers and each layer can have a different number of neurons.

There are also different types of layers. The first layer is always called input layer and the last layer output layer. Everything between is a hidden layer. However, layers are different from each other through different activation functions (see below), pooling etc. Typically each neuron within one layer has the same activation function, though, meaning the layers itself are uniform.

Activation functions

An activation function is a function that is applied to the output of a single neuron.

One example is the rectified linear activation function or sometimes called a rectified linear unit. It calculates $max(0, y)$, so it sets all negative values to 0. That is useful in cases, where a negative value would make no sense in the context.